


"Presidential Address: The Value of Theory in Consumer Research". Journal of Experimental Psychology: Learning, Memory, and Cognition. "Effects of strategy instructions and practice on nine-dot problem solving". ^ Lung, Ching-tung Dominowski, Roger L."Locating the Difficulty in Insight Problems: Individual and Sex Differences". ^ Daniel Kies, "English Composition 2: Assumptions: Puzzle of the Nine Dots", retr.^ "Sam Loyd's Cyclopedia of 5000 Puzzles, Tricks, and Conundrums With Answers".Travers, The Puzzle-Mine: Puzzles Collected from the Works of the Late Henry Ernest Dudeney. ^ Facsimile from Cyclopedia of Puzzles - Columbus's Egg Puzzle is on right-hand page."Chapter 9: Sam Loyd: America's Greatest Puzzlist". ^ "Advertising for Elgin Creamery Co".The Twentieth Century Standard Puzzle Book. "Unicursal Polygonal Paths And Other Graphs On Point Lattices".
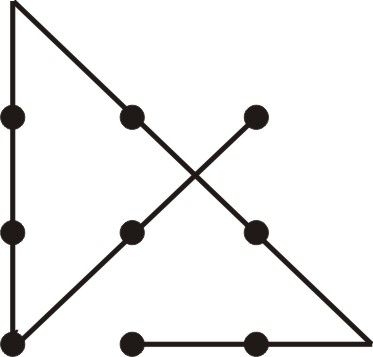
Polygonal Path Covering N X N Lattice Of Points, Queen's Tours, etc". "Sources In Recreational Mathematics, An Annotated Bibliography (8th preliminary edition): 6.AK. Place the queen wherever you want, make her go through all the squares of the chessboard by regular steps, and bring her back to her starting point at the fourteenth move. Placer la Dame ot l'on voudra, lui faire parcourir par des marches suivies et régulières toutes les cases de I'échiquier, et la ramener au quatorzième coup à son point de départ. Le Sphinx: Journal des échecs (in French). The Nine Dots Prize, named after the puzzle, is a competition-based prize for "creative thinking that tackles contemporary societal issues." It is sponsored by the Kadas Prize Foundation and supported by the Cambridge University Press and the Centre for Research in the Arts, Social Sciences and Humanities at the University of Cambridge. Finally, various results for the a × b array of dots are proven. Moreover, the further constraint that the closed path remain within the convex hull of the array of dots can be satisfied for all n > 5. Golomb and John Selfridge showed that the unicursal polygonal path of 2 n - 2 segments exists on the n × n array for all n > 3 with the further constraint that the path be closed, i.e., it starts and ends at the same point. In 1956, the conjecture was proven by John Selfridge. Klamkin showed that if n > 2, then 2 n - 2 line segments are sufficient and conjectured that it is necessary too. Various such extensions were stated as puzzles by Dudeney and Loyd with different added constraints. If, instead of the 3-by-3 square lattice, we consider the n-by- n square lattice, then what is the least amount of lines needed to connect the dots without lifting the pen? Or, stated in mathematical terminology, what is the minimum- segment unicursal polygonal path covering the n × n array of dots? It is also possible to fold the paper flat, or to cut the paper into pieces and rearrange it, in such a way that the nine dots lie on a single line in the plane. Thus a single line can be drawn connecting all nine dots-which would appear as three lines in parallel on the paper, when flattened out. Īnother way to use only a single line involves rolling the paper into a three-dimensional cylinder, so that the dots align along a single helix (which, as a geodesic of the cylinder, could be considered to be in some sense a straight line). Or, if the line is allowed to be arbitrarily thick, then one line can cover all of the points. If the dots are assumed to have some finite size, rather than to be infinitesimally-small mathematical grid points, then it is possible to connect them with only three slightly-slanted lines. Various published solutions break the implicit rules of the puzzle in order to achieve a solution with even fewer than four lines. The inherent difficulty of the puzzle has been studied in experimental psychology. According to Daniel Kies, the puzzle seems hard because we commonly imagine a boundary around the edge of the dot array. The phrase thinking outside the box, used by management consultants in the 1970s and 1980s, is a restatement of the solution strategy. To do so, one goes outside the confines of the square area defined by the nine dots themselves. It is possible to mark off the nine dots in four lines.


 0 kommentar(er)
0 kommentar(er)
